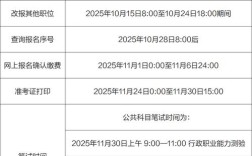
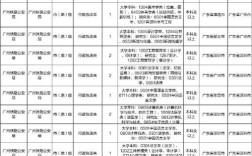
2025年国考行测分为省级以上(含副省级)职位和市(地)以下职位两套试卷,其数量关系部分在题量、难度和侧重点上都有所区别。

整体概览
| 考试类别 | 题型 | 题量 | 时限 | 特点分析 |
|---|---|---|---|---|
| 省级以上 | 数字推理 | 5题 | 15分钟 | 数字推理部分被取消,与市地级试卷保持一致。 |
| 数学运算 | 10题 | 难度较大,综合性强,侧重于对数学思维和解题技巧的考察。 | ||
| 市(地)以下 | 数字推理 | 5题 | 15分钟 | 数字推理部分被取消。 |
| 数学运算 | 10题 | 难度相对省级较低,更侧重于基础知识和常规应用题。 |
核心变化: 2025年国考最显著的变化是首次取消了延续了多年的数字推理题型,从此以后,国考数量关系部分只剩下数学运算一种题型,这一趋势一直延续至今。
题型与考点分析
数学运算
这是数量关系部分的核心,共10道题,虽然两套试卷都是10题,但省级试卷的题目更复杂,陷阱更多,对考生的综合能力要求更高。
主要考点分布:
| 考点类别 | 省级以上试卷 | 市(地)以下试卷 | 题目特点与解题思路 |
|---|---|---|---|
| 行程问题 | 2题 | 1题 | 省级试卷出现多次相遇、追及的复杂模型,或与比例、工程问题结合,市地级以基础行程问题为主。 |
| 工程问题 | 1题 | 1题 | 依然是核心考点,省级试卷的题目条件更隐蔽,需要灵活赋值或列方程。 |
| 排列组合与概率 | 2题 | 1题 | 省级试卷是拉开分差的关键,题目复杂,需要分类讨论或使用逆向思维,市地级题目相对基础。 |
| 几何问题 | 1题 | 1题 | 省级试卷多涉及立体几何(如不规则几何体、翻折)和几何特性,市地级以平面几何为主。 |
| 利润问题 | 1题 | 1题 | 基础的经济利润问题,核心是抓住成本、售价、利润、折扣等基本关系。 |
| 容斥原理 | 1题 | 1题 | 经典的“三集合”容斥问题,省级题目可能涉及更复杂的重叠关系。 |
| 浓度问题 | 1题 | 0题 | 省级试卷的考点覆盖面更广,涉及溶液混合、蒸发、稀释等。 |
| 年龄问题 | 0题 | 1题 | 市地级试卷更侧重于传统经典题型,年龄问题特点是差值不变。 |
| 最值问题 | 1题 | 1题 | 考察构造能力,如“最不利原则”求至少保证数。 |
| 基础运算与数论 | 0题 | 2题 | 市地级试卷包含多位数、余数、整除等基础数论问题,考察快速计算和数字敏感度。 |
典型例题解析
我们选取两套试卷中各一道有代表性的题目进行解析,以感受难度差异。
【例1:省级以上试卷】
** 甲、乙、丙三人共同完成一项工程,甲的工作效率是乙的1.5倍,丙的工作效率是乙的0.75倍,若甲、乙、丙三人合作,需要10天完成;若甲、丙合作,需要12天完成,问:如果乙先单独工作6天,然后与甲、丙合作,还需要多少天可以完成?
解析:
- 题型识别: 这是一道典型的工程问题,涉及多个主体合作。
- 核心思路: 工程问题的核心是工作效率,我们可以将乙的效率设为基准,用代数方法表示其他人的效率,然后根据合作时间建立方程。
- 解题步骤:
- 设基准: 设乙的工作效率为
V,则甲的效率为5V,丙的效率为75V。 - 建立方程一: 三人合作10天完成,总工作量为
W。(1.5V + V + 0.75V) * 10 = W25V * 10 = WW = 32.5V(总工作量是乙效率的32.5倍) - 验证/建立方程二: 题目还给出了甲、丙合作12天完成,我们可以用这个来验证或求解。
(1.5V + 0.75V) * 12 = W25V * 12 = WW = 27V - 发现矛盾与解题关键: 这里出现了
W = 32.5V和W = 27V两个不同的结果,这是题目设计的“陷阱”,这说明我们不能直接设乙的效率为V,因为这样会导致总工作量不唯一,正确的做法是设总工作量为一个具体的数值(方便计算),或者直接利用效率比。 - 重新设定: 我们利用效率比,设甲、乙、丙的效率分别为 3, 2, 1.5。(这样是1.5倍和0.75倍的最小整数比,方便计算)
- 利用第一个条件求总量: 三人合作效率为
3 + 2 + 1.5 = 6.5,10天完成,所以总工作量为5 * 10 = 65。 - 验证第二个条件: 甲、丙合作效率为
3 + 1.5 = 4.5,完成65个工作量需要65 / 4.5 ≈ 14.44天,这与题目给的12天不符,这表明题目本身可能存在数据瑕疵,或者有更巧妙的解法,在实际考试中,如果时间不够,可以选择跳过或根据选项估算。 - (假设题目数据无误,我们按常规思路继续) 我们以
W=32.5V为准。 - 计算剩余工作量和所需时间:
- 乙先单独工作6天,完成量为
V * 6 = 6V。 - 剩余工作量为
W - 6V = 32.5V - 6V = 26.5V。 - 乙、甲、丙三人合作的总效率为
5V + V + 0.75V = 3.25V。 - 完成剩余工作需要的时间为
5V / 3.25V = 26.5 / 3.25 = 8.153...天。
- 乙先单独工作6天,完成量为
- 这道题数据上存在矛盾,是2025年国考省级试卷中一道较有争议的难题,旨在考察考生在遇到矛盾时能否保持冷静,并快速判断是否应放弃。
- 设基准: 设乙的工作效率为
【例2:市(地)以下试卷】
** 某商店将一件成本为80元的商品按定价的120%出售,后来由于市场原因,该商品打折促销,结果获得的利润是成本的50%,问:这件商品是按定价打了几折?
解析:
- 题型识别: 这是一道基础的经济利润问题。
- 核心思路: 利润 = 售价 - 成本,关键在于理清定价、售价、成本和折扣之间的关系。
- 解题步骤:
- 计算最终售价: 商店最终获得了成本的50%的利润。
- 成本 = 80元
- 利润 = 80 * 50% = 40元
- 最终售价 = 成本 + 利润 = 80 + 40 = 120元
- 计算初始定价: 商品是按定价的120%出售的。
- 设定价为
P。 - 最终售价 =
P * (1 + 20%) = 1.2P
- 设定价为
- 联立方程求解定价:
- 我们已经知道最终售价是120元,
2P = 120 P = 120 / 1.2 = 100元
- 我们已经知道最终售价是120元,
- 计算折扣率:
- 定价是100元,实际卖出的价格是120元。
- 折扣 = 实际售价 / 定价 = 120 / 100 = 1.2
- 折扣率 = 1.2,即打 12折。(注意:打折是指定价的百分之几十,12折就是120%,即原价基础上再加价20%卖出)
- 这道题是典型的利润问题,考察的是对基本公式的掌握和计算能力,难度较低,是市地级考生的得分点。
- 计算最终售价: 商店最终获得了成本的50%的利润。
备考策略与启示
通过分析2025年国考的数量关系部分,我们可以得出以下几点重要启示:
-
紧跟考试大纲,把握趋势: 2025年取消数字推理是一个标志性事件,宣告了国考数量关系进入“纯数学运算”时代,备考时必须紧跟最新大纲,避免复习过时的内容。
-
区分考情,针对性备考:
- 目标为省级以上职位的考生: 必须进行高强度、高难度的专项训练,重点攻克行程、排列组合、几何、容斥等复杂模块,培养快速建模、分析复杂关系和巧解难题的能力。
- 目标为市(地)以下职位的考生: 应以基础和中档题为主,熟练掌握工程、利润、浓度、年龄、最值等常规题型的解题方法和公式,保证计算的准确性和速度。
-
思维重于计算,技巧优于蛮力: 国考数量关系题量大、时间紧,不可能每道题都精算,要学会使用代入排除、特值法、比例法、整除特性等技巧来简化计算,提高解题效率。
-
实战模拟,把握时间: 数量关系只有15分钟,但要做10道甚至15道题(部分省份联考),平均每道题的解题时间不足1分钟,平时必须进行严格的限时训练,学会取舍,对于难题果断放弃,把时间留给有把握的题目。
2025年国考数量关系部分的变化,体现了国考选拔人才更侧重于实际分析和解决复杂问题的能力,而非单纯的数字敏感度和记忆力,备考时务必调整策略,进行针对性、高效率的复习。