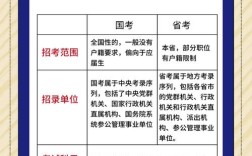
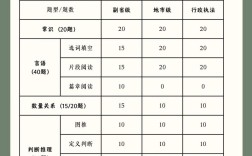
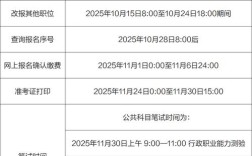
国考的推理题主要考察考生的逻辑思维能力、分析判断能力和信息处理能力，它不是考察高深的逻辑学理论,而是考察在日常生活中和工作中运用逻辑常识解决问题的能力。

下面我将从题型分布、核心考点、解题技巧和经典例题四个方面,为你详细解析国考推理题。

题型分布

国考行测的推理题主要集中在以下几个部分：

1. 判断推理：这是推理题的“主战场”，占比最高,通常包含四个模块：

   • 图形推理：通过观察图形的规律,选出最符合规律的下一个图形。
   • 定义判断：给一个概念的定义,然后根据定义判断选项是否符合。
   • 类比推理：给出一组或多组相关的词语,要求考生在备选答案中找出与之在逻辑关系上最为贴近或相似的一组。
   • 逻辑判断：也叫“演绎推理”，通常由一段题干和多个选项组成，要求考生根据题干信息,选择最能从题干中推出或不能推出的结论。

2. 言语理解与表达：部分题目也蕴含着推理过程。

   • 语句表达：如下文提到的“语句排序题”,需要理清句子间的逻辑关系。
   • 逻辑填空：虽然考的是词语，但需要根据上下文的逻辑关系（如因果、转折、递进、并列）来选择最恰当的词语。

3. 常识判断：虽然以知识性为主，但很多题目也需要进行简单的逻辑推理才能得出正确答案,而不是死记硬背。

核心考点解析

（一）图形推理

图形推理的核心是“找规律”,规律主要分为以下几类：

1. 数量规律：

   • 点、线、面、角：数图形中的交点数、线条数（直线、曲线）、封闭区域数、角的数量等。
   • 元素种类/个数：看图形中出现了多少种不同的元素,或者某个元素的数量。
   • 部分数：看图形被分成了几个不相连的部分。

2. 位置规律：

   • 平移：图形在平面内进行上下、左右、顺时针/逆时针移动。
   • 旋转：图形围绕某个点进行旋转。
   • 翻转：图形进行轴对称翻转。
   • 嵌套：一个图形在另一个图形内部,且两者都可能发生位置变化。

3. 样式规律：

   • 叠加：两个图形通过“求同”、“求异”或“规律叠加”得到第三个图形。
   • 遍历：一组图形中,所有可能的元素或样式都会完整地出现一遍。
   • 运算：图形内部进行加减乘除等运算。

4. 属性规律：

   • 对称性：轴对称、中心对称。
   • 曲直性：全直线、全曲线、曲直混合。
   • 开闭性：开放图形、封闭图形。

5. 特殊规律：

   • 空间重构：给一个展开的平面图，问能折成哪个立体图形（“折纸盒”问题）。
   • 三视图：从主视图、俯视图、侧视图的角度观察立体图形。

（二）定义判断

解题关键：“紧扣定义，不附加常识”。

1. 快速拆解定义：将定义拆解为“主体、客体、条件、原因、方式/手段、结果”等要素。
2. 抓住关键词：定义中的“……是……”、“指”、“即”等后面的内容通常是核心要点，以及“必须”、“只有”、“所有”等限定词。
3. 对比选项：将选项与定义的各个要素进行比对，寻找“不符合”的要素,从而排除错误选项。

（三）类比推理

解题关键：“找词项间的逻辑关系”。

1. 逻辑关系：

   • 全同关系：如：西红柿 -> 番茄
   • 并列关系：如：苹果 -> 香蕉（水果）；鲁迅 -> 巴金（作家）
   • 包容关系（种属）：如：电脑 -> 电子设备（电脑是电子设备的一种）
   • 交叉关系：如：医生 -> 博士（有的医生是博士,有的不是）
   • 对应关系：这是最常见的。
     • 功能对应：如：笔 -> 书写
     • 职业与工具：如：医生 -> 听诊器
     • 材料与成品：如：木材 -> 家具
     • 因果/条件关系：如：努力 -> 成功
     • 组成关系：如：电脑 -> CPU
     • 象征/比喻关系：如：鸽子 -> 和平

2. 关系层层递进：有时需要分析多组词之间的关系，如“医生：医院”是“职业：工作场所”关系,选项中也要找类似的。

（四）逻辑判断

这是逻辑考察的重中之重，题型多样,但核心是形式逻辑和论证逻辑。

1. 翻译推理：

   • 核心：将日常语言翻译成逻辑符号（..就...、只有...才...、且、或等）。
   • 规则：熟练掌握“逆否命题”（原命题和逆否命题等价）、“德摩根定律”（-(A且B) = -A或-B）等。

2. 真假推理：

   • 核心：题干中给出几句话，其中只有一句为真（或只有一句为假）,要求推出结论。
   • 方法：找矛盾关系（必有一真一假）、找反对关系（可以同真/同假）,然后进行假设和排除。

3. 归纳推理：

   • 核心：从题干的具体信息,概括出一般性结论。
   • 原则：
     • 话题一致：结论必须与题干讨论的话题一致。
     • 从弱原则：优先选择可能性、确定性较弱的选项（如“可能”、“有些”），避免选择“必然”、“所有”等绝对化表述。
     • 不引申：结论不能脱离题干信息进行主观臆断。

4. 加强/削弱论证：

   • 核心：识别题干的“论点”和“论据”,然后判断选项是在支持还是在反驳论点。
   • 加强方式：
     • 搭桥：建立论点和论据之间的联系。
     • 补充论据：提供新的证据,证明论点的正确性。
     • 排除他因：说明没有其他因素影响结果。
   • 削弱方式：
     • 否定论点：直接说明论点是错的。
     • 拆桥：切断论点和论据之间的联系。
     • 否定论据：说明论据不真实或不可靠。
     • 另有他因：指出是其他因素导致了结果的发生。

解题技巧与备考建议

1. 系统学习，掌握理论：不要盲目刷题，先系统地学习逻辑学的基本概念和规则，特别是逻辑判断部分，知道“逆否命题”、“矛盾关系”是什么,才能快速识别和运用。

2. 大量刷题，总结规律：理论学完后，通过大量刷题来巩固，特别是图形推理和类比推理，需要培养“题感”，做完题后，一定要复盘，总结每道题的考点和解题思路，建立自己的“错题本”。

3. 提高阅读速度和理解能力：对于定义判断和逻辑判断，题干往往较长，要学会快速抓取关键信息,理解核心意思。

4. 保持严谨，避免“想当然”：国考的逻辑题非常严谨，不能凭生活经验或常识去判断，尤其是定义判断,一切以题干给出的定义为准。

5. 时间管理：推理题虽然重要，但也很耗时，要学会取舍，遇到难题不要钻牛角尖，果断跳过,先把会做的题拿到分。

经典例题解析

例1：图形推理

从所给的四个选项中，选择最合适的一个填入问号处,使之呈现一定的规律性。

[图1: 一个圆]  [图2: 一个正方形]  [图3: 一个三角形]
[图4: 两个相交的圆]  [图5: 两个嵌套的正方形]  [图6: ?]

A. 一个五边形 B. 两个相交的三角形 C. 一个星形 D. 两个分离的三角形

解析： 这道题考察的是数量规律中的元素种类/个数。

• 观察前三行：第一行都是1个元素,第二行都是2个元素。
• 观察第三行，第一个图是1个元素，第二个图是2个元素，那么问号处应该是1个元素。
• 再观察元素样式：第一行是圆形，第二行是方形，第三行是三角形，所以问号处应该是一个三角形。
• 综合来看，需要一个由1个元素构成的三角形图形。
• 选项A、C是1个元素，但不是三角形，B是2个元素,D是2个元素。
• 等等，让我们重新审视。 可能规律不是这么简单。
• 再试一次：我们看每一行图形的“构成部分”。
  • 第一行：圆（1个部分）、正方形（1个部分）、三角形（1个部分）,数量都是1。
  • 第二行：两个相交的圆（2个部分）、两个嵌套的正方形（2个部分）、？,数量应该是2。
  • 第三行：一个五角星（复杂图形，但通常看作1个部分）、一个星形（1个部分）、？,数量应该是1。
• 这个规律似乎更合理，但题目通常只有一行规律,我们再看另一种可能。
• 核心规律：这道题最经典的规律是“图形的对称轴数量”。
  • 圆：无数条对称轴。
  • 正方形：2条对称轴。
  • 三角形：1条对称轴。
  • 两个相交的圆：2条对称轴。
  • 两个嵌套的正方形：2条对称轴。
  • 规律：每一行的图形，其对称轴数量之和是固定的，第一行：无数+2+1 = 无穷（不对）。
• 换个思路：看“曲直性”。

  第一行：圆（曲）、正方形（直）、三角形（直）,没有明显规律。

• 回归最简单的规律：“元素数量”。
  • 第一行：1, 1, 1
  • 第二行：2, 2, ?
  • 第三行：1, 1, ?
  • 如果是按行规律,那么问号处应该是2个元素。
  • 如果是按列规律，第一列：1, 2, 1，第二列：1, 2, 1，第三列：1, ?, ?，所以问号处应该是1个元素,这又矛盾了。
• 重新审视题目描述：通常这种题是“九宫格”或“三行三列”，如果题目是“三行”，每行三个图，那么规律很可能是“每一行的图形，其构成部分的数量相等”。
  • 第一行：1, 1, 1
  • 第二行：2, 2, 2
  • 第三行：1, 1, 1
  • 所以问号处应该是1个元素。
  • 再看元素样式，第一行是圆形，第二行是方形，第三行是三角形，所以问号处应该是1个三角形。
  • 在选项中，A. 一个五边形（1个，但样式不对），C. 一个星形（1个，样式不对）。B. 两个相交的三角形（2个，数量不对），D. 两个分离的三角形（2个，数量不对）。
• 这说明我的假设或题目本身可能有误。 让我们换一个经典真题的思路。

经典真题改编版：

[图1: O] [图2: □] [图3: △]
[图4: OO] [图5: □□] [图6: ?]

A. △△ B. △△ (相交) C. ☆ D. ◇

解析：

• 规律：每一行的图形，其构成部分的数量相同。
• 第一行：圆(1)、正方形(1)、三角形(1),数量为1。
• 第二行：两个圆(2)、两个正方形(2)、？,数量为2。
• 第三行：一个星形(1)、一个菱形(1)、？,数量为1。
• 第二行的问号处应该是2个元素，第三行的问号处应该是1个元素。
• 如果你的问题是第二行的问号，那么应该选A或B，如果问题是第三行的问号，那么应该选C或D。
• 再看样式：第一行是基础图形，第二行是基础图形的重复，第三行是复杂图形,所以问号处也应是复杂图形。
• 如果问题是第三行，选C或D，如果题目是“选择一个填入？”，通常指最后一个，即第三行第三个，那么选C或D中的一个,这又回到了起点。

图形推理的规律需要多角度尝试，对于这个模糊的例子，最可能且最简单的规律是“每行元素数量相同”，如果问号在第二行，选2个元素；在第三行，选1个元素，同时结合样式变化,就能选出答案。

例2：逻辑判断（加强/削弱）

研究发现，经常喝咖啡的人患帕金森病的风险比不喝咖啡的人低,喝咖啡有助于预防帕金森病。

以下哪项如果为真,最能削弱上述结论？

A. 咖啡中含有的某种化学物质可以抑制导致帕金森病的脑部神经元的退化。 B. 有些人不喝咖啡，但通过其他方式摄入了咖啡中的关键成分，他们患帕金森病的风险也较低。 C. 经常喝咖啡的人通常也具有其他更健康的生活习惯，如规律锻炼和均衡饮食。 D. 帕金森病的发病机制非常复杂,目前尚未完全明确。

解析：

• 论点：喝咖啡有助于预防帕金森病。

• 论据：经常喝咖啡的人患帕金森病的风险比不喝咖啡的人低。

• 论证过程：从“喝咖啡”和“患病率低”这两个现象，推断出“喝咖啡是导致患病率低的原因”，这是一个典型的因果论证。

• 分析选项：

  • A. 咖啡中含有的某种化学物质可以抑制导致帕金森病的脑部神经元的退化。
    • 这是在解释为什么喝咖啡能预防帕金森病，指出了其中的原理，这属于加强论证，是搭桥或补充论据,而不是削弱。
  • B. 有些人不喝咖啡，但通过其他方式摄入了咖啡中的关键成分，他们患帕金森病的风险也较低。

    这说明真正起作用的不是“喝咖啡”这个行为，而是咖啡中的“关键成分”，这为“喝咖啡预防帕金森病”提供了另一种解释，但并没有直接削弱“喝咖啡”和“预防”之间的因果联系，它甚至可以看作是一种间接的加强,削弱力度较弱。

  • C. 经常喝咖啡的人通常也具有其他更健康的生活习惯，如规律锻炼和均衡饮食。
    • 这提出了一个“另有他因”，它指出，经常喝咖啡的人患病率低，可能不是因为咖啡本身，而是因为他们还有“规律锻炼、均衡饮食”等其他健康习惯，这些习惯才是真正降低患病风险的原因，这就直接削弱了“喝咖啡”是原因的结论，是最强的削弱项。
  • D. 帕金森病的发病机制非常复杂，目前尚未完全明确。
    • 这是在质疑我们对帕金森病的认知程度，属于话题转移，它没有直接针对“喝咖啡”和“帕金森病”之间的关系进行削弱,因此削弱力度最弱。

• 最终答案：C

希望这份详细的解析能帮助你更好地理解和准备公务员国考中的推理题！祝你成功！