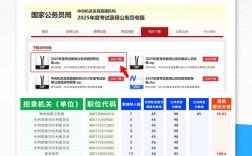
题目回顾
从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。 图形：**
【第一组】
[A] [B] [C]
[◯] + [△] = [◯△]
【第二组】
[◯△] + [▢] = [?]
【选项】
[1] [◯▢] [2] [△▢] [3] [◯△▢] [4] [空白](注：这里的 [ ] 和文字是为了方便描述，实际考试中是标准的几何图形。)
（图片来源网络，侵删）
解题思路
这道题属于典型的“图形叠加”类问题，解决这类问题的关键是观察第一组图形的运算规律,然后将该规律应用到第二组图形中。
第一步：分析第一组图形，找出规律
第一组图形由三个部分组成：两个独立的图形（一个圆 ◯ 和一个三角形 △）以及它们运算后得到的结果（一个圆和一个三角形组合的图形 ◯△）。
我们需要思考，“◯” + “△” = “◯△” 这个运算遵循了什么规则？
（图片来源网络，侵删）
观察可以发现，运算后的图形包含了两个原始图形的所有元素（一个圆和一个三角形），并且这些元素没有发生位置上的重叠或改变，它们只是被简单地“组合”或“叠加”在了一起。
我们可以总结出第一组图形所揭示的运算规律是：将两个图形进行叠加，保留两个图形中的所有元素。
第二步：将规律应用到第二组图形
我们将这个规律应用到第二组图形。
（图片来源网络，侵删）
第二组图形的运算式是：[◯△] + [▢] = [?]
根据我们总结的规律：
- 第一个图形是 [◯△]，它本身已经包含了“圆”和“三角形”两个元素。
- 第二个图形是 [▢]，它是一个“正方形”元素。
- 进行叠加运算：我们需要将第一个图形中的所有元素（圆、三角形）和第二个图形中的所有元素（正方形）全部保留下来,进行组合。
最终的结果图形应该同时包含：一个圆 (◯)、一个三角形 (△) 和一个正方形 (▢)。
第三步：对比选项，选出正确答案
现在我们来查看四个选项，哪个图形同时包含了圆、三角形和正方形：
- [1] [◯▢]：只包含圆和正方形，缺少三角形,不符合。
- [2] [△▢]：只包含三角形和正方形，缺少圆,不符合。
- [3] [◯△▢]：同时包含了圆 (◯)、三角形 (△) 和正方形 (▢),完全符合我们的推理结果。
- [4] [空白]：没有任何元素,不符合。
最合适、最符合规律的就是选项 [3]。
本题的核心考点是 “图形叠加中的元素组合”，具体来说是 “元素相加” 或 “元素求和”，这类规律要求将两个图形的所有元素全部保留,合并成一个新的图形。
- 规律：图形叠加,保留所有元素。
- 应用：(A+B) + C = A+B+C。
- 答案：C (在原题选项中是第3个)。 是国考图形推理中的常见题型，关键在于快速识别出图形之间的运算关系,并准确提炼出其中的规律。
