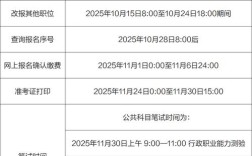
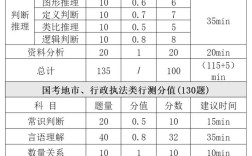
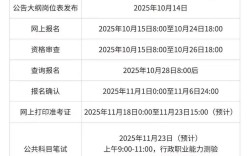
题型概述
形式** 给你一个由六个面组成的平面展开图(通常称为“六面体”或“立方体”),以及四个由这六个面折叠而成的立体图形选项,要求你判断哪个选项是正确折叠而成的。
核心考点 主要考察考生的空间想象能力和逻辑推理能力,你需要快速地在脑中将平面图“折叠”成立体图,或者通过分析平面图的相邻关系,来排除错误选项。

难度分析 这是图形推理中难度较高的一类题目,因为:
- 没有固定的解题公式。
- 空间想象能力因人而异,难以短期速成,看似复杂,信息量大。
解题策略 核心思想:利用“相对面”和“相邻面”的关系进行排除。 我们的目标不是把所有可能性都想象出来,而是通过快速识别出“不可能”的情况,来缩小范围,最终找到唯一正确的答案。
核心解题技巧
这是本部分的重中之重,请务必理解并熟练掌握。
相对关系法(最快速、最有效的排除工具)
快速判断相对面 在六面体的平面展开图中,三组相对面有以下两种常见的分布模式:

-
“1-1-1”分布(隔一个): 三个相对面在展开图上,两两之间隔着一个其他面。
- 在“Z”字形或“一”字形的展开图中,两端的两个面是相对的。
- 口诀: 相间排列的两个面是相对面。
-
“1-2-2”分布(隔两个): 三个相对面在展开图上,两个面被两个其他面隔开。
- 在“田”字形的展开图中,位于对角线的两个面是相对的。
- 口诀: 隔一个面(“日”字形)的两个面是相对面。
如何应用相对面进行排除? 核心原则: 在立体图形中,相对面不能同时被看到。
-
同时看到两个相对的面
 (图片来源网络,侵删)
(图片来源网络,侵删)- 如果在某个选项中,你同时看到了两个在平面展开图上是相对关系的面,那么这个选项一定错误,直接排除。
-
三个面两两相邻,但其中一对是相对面
- 这是一种稍微隐蔽的情况,如果选项中给出的三个公共顶点(或公共边)的面,其中有两个在平面图上是相对的,那么这个选项也一定错误,因为如果这两个面相邻,那么它们的第三个面(公共顶点所对的面)就无法与它们同时相邻。
示例: 假设在平面展开图中,A和F是相对面,B和D是相对面,C和E是相对面。
- 错误选项1: 一个立体图形中同时出现了A面和F面。 → 排除。
- 错误选项2: 一个立体图形中同时出现了B面和D面。 → 排除。
- 错误选项3: 一个立体图形中,A、B、C三个面两两相邻,但A和C是相对面。 → 排除。
相邻关系法(在相对面无法排除时使用)
当所有选项都满足“相对面没有同时出现”时,我们就需要使用相邻关系法来进一步筛选。
确定公共边/公共顶点
- 公共边: 两个相邻的平面图形在折叠后会共享一条边。
- 公共顶点: 三个相邻的平面图形在折叠后会共享一个顶点。
如何应用相邻面进行验证? 核心原则: 两个相邻面的相对位置是固定的。
- 方法:折纸法
- 选定一个面作为基准面(通常是题目中给出的、位置最明确的面)。
- 想象或动手“折叠”:将与基准面相邻的面沿着公共边“折”起来。
- 观察方向:折叠后,相邻面的图案、箭头、文字等方向是否与选项中的方向一致。
示例: 假设我们有一个基准面“上”,它的右边是“前”,下面是“右”,当我们把“前”和“右”都沿着与“上”的边折起来后,“前”和“右”这两条边也会在空间中相遇,观察“前”和“右”这两个面的图案方向,是否与选项中这两个面相邻时的方向一致,如果不一致,则该选项错误。
解题步骤与实战演练
标准解题流程:
-
第一步:看选项,找矛盾。
- 快速扫描四个选项,看是否有“1-2-1”、“2-2-2”(即同时出现两对或三对相对面)的情况,这是最快排除错误选项的方法。
-
第二步:若无法排除,用相对关系法。
- 在心中默念或快速标记出平面图中的三组相对面。
- 检查每个选项,看是否存在“同时出现一对相对面”的情况,有则排除。
-
第三步:若只剩一项或多项,用相邻关系法。
- 从剩下的选项中,任选一个进行验证。
- 选择一个最易识别的面作为基准(带箭头的、有文字的、图案不对称的)。
- 使用“折纸法”,验证其相邻面的相对位置和方向是否与选项完全一致。
- 逐一验证,直到找到唯一正确的答案。
真题示例与解析
假设我们有这样一个平面展开图(为了方便,我们用字母代替):
步骤1:判断相对面
- 观察这个“Z”字形展开图。
- A和F是相对面(隔一个)。
- B和D是相对面(隔一个)。
- C和E是相对面(隔一个)。
步骤2:分析选项(假设四个选项如下)
-
选项A:
- 假设这个立体图形能看到A、B、C三个面。
- 检查:A和B是相邻的,A和C是相邻的,B和C也是相邻的,没有出现相对面,暂时保留。
-
选项B:
- 假设这个立体图形能看到A、B、D三个面。
- 检查:A和B是相邻的,A和D是相邻的,但B和D是相对面!它们在立体图中却同时出现了,并且还相邻,这绝对不可能。
- 排除B选项。
-
选项C:
- 假设这个立体图形能看到A、C、D三个面。
- 检查:A和C是相邻的,A和D是相邻的,但C和D是相邻的吗? 我们需要看它们的公共顶点。
- 在平面图中,C和D并不直接相邻,它们通过A和E/B间接相连,在立体图中,如果A、C、D要两两相邻,它们的公共顶点关系必须成立,通过想象或折纸,你会发现C和D无法同时与A相邻而不发生冲突,更简单的方法是,看A、C、D这三个面,其中C和D在平面图上不是直接相邻的,但在选项中它们却以某种方式“挤”在了一起,这通常是错误的。
- 排除C选项。(此题更严谨的做法是相邻关系法,但相对面法已经排除了一个,剩下两个通常一个明显错误一个正确)
-
选项D:
- 假设这个立体图形能看到A、C、E三个面。
- 检查:A和C是相邻的,A和E是相邻的,但C和E是相对面!它们在立体图中却同时出现了。
- 排除D选项。
最终答案:A
备考建议
- 心态放平:这类题确实难,不要因为做不出来而焦虑,它本身就是用来拉开分数差距的。
- 先易后难:在考场上,如果一道折叠题想了30秒还没头绪,果断标记并跳过,先做后面的题。
- 专项训练:找大量的真题进行练习,形成条件反射,看到图就能快速反应出相对面。
- 动手实践:准备一些便利贴,自己动手折一折,把抽象的空间想象变为具体的触觉感知,对建立空间感非常有帮助。
- 总结规律:除了“1-1-1”和“1-2-2”分布,还有其他不规则的展开图,多做练习,总结更多识别相对面的技巧。
希望这份详细的指南能帮助你攻克国考中的图形折叠题!祝你成功上岸!