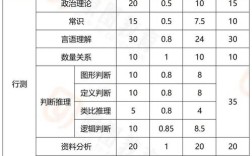
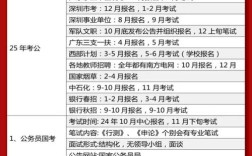
虽然近年来国考行测中直接考查“数字推理”的频率有所降低，但在一些省份的省考、事业单位考试以及军队文职等考试中，这类题型依然是重点，掌握数列规律对于培养逻辑思维、快速发现数据之间的联系非常有帮助，这种能力在解决其他资料分析、数学运算问题时同样至关重要。

国考数列题的核心特点是：规律性强、形式多样、注重思维灵活性，下面我将通过“题型分类 + 解题技巧 + 经典例题”的方式,为你系统梳理。

核心解题技巧（通用）

在看具体题型前，先掌握几个通用的“破题”步骤,可以帮你更快地找到突破口：

1. “看”特征：快速扫视数列,判断其是否为：

   • 单调递增/递减：数字是越来越大还是越来越小？
   • 波动变化：数字是不是忽大忽小？
   • 整数/分数/小数：数字的属性是什么？
   • 长数列/短数列：数列长度是5项以上还是5项以下？长数列（6项及以上）通常规律更复杂,可能涉及多级运算或组合规律。

2. “做”差商：这是最核心、最常用的方法。

   • 作差：对相邻两项进行减法，得到一个新数列（一级差数列），如果新数列没有明显规律，对新数列再作差，得到二级差数列,以此类推。
   • 作商：如果数列增长速度非常快（通常是倍数关系），考虑对相邻两项进行除法,得到一个等比数列或其他规律。

3. “想”特殊：如果作差/作商没有效果,思考是否有以下特殊规律：

   • 质数/合数：数列是否与质数相关？
   • 周期：数字是否按照某个固定长度（如3, 5）的周期循环？
   • 图形：是否为“九宫格”形式的数列，需要从行、列、对角线找规律？
   • 分组：奇数项和偶数项是否分别有规律？
   • 倍数关系：后一项是否是前一项的倍数加上/减去一个数？

4. “拆”数字：当数字本身比较“大”或比较“怪”时，考虑将其拆分成更小的部分（如个位、十位、百位，或者进行因数分解）。

主要题型分类与例题解析

等差数列（及其变式）

这是最基础的数列，特点是相邻两项的差是一个常数，变式则指这个“差”本身构成了一个新的等差数列或其他简单数列。

例题1（基础等差数列） 数列： 3, 7, 11, 15, ( ) 解析： 这是一个典型的等差数列，后项减去前项的差均为4。 7 - 3 = 4 11 - 7 = 4 15 - 11 = 4 括号内的数字应为 15 + 4 = 19。

例题2（二级等差数列） 数列： 2, 5, 10, 17, 26, ( ) 解析：

1. 作差：相邻两项的差为： 5 - 2 = 3 10 - 5 = 5 17 - 10 = 7 26 - 17 = 9
2. 观察新数列：得到的新数列是 3, 5, 7, 9,这是一个以2为公差的等差数列。
3. 推导：下一个差应该是 9 + 2 = 11。
4. 求解：括号内的数字应为 26 + 11 = 37。

例题3（三级等差数列） 数列： 1, 2, 6, 15, 31, ( ) 解析：

1. 作差：相邻两项的差为： 2 - 1 = 1 6 - 2 = 4 15 - 6 = 9 31 - 15 = 16
2. 观察新数列：得到的新数列是 1, 4, 9, 16，这是完全平方数（1², 2², 3², 4²）。
3. 推导：下一个差应该是 5² = 25。
4. 求解：括号内的数字应为 31 + 25 = 56。

等比数列（及其变式）

特点是相邻两项的商是一个常数，变式则指这个“商”本身构成了一个新的等比数列,或者前一项乘以一个常数再加减一个数得到后一项。

例题4（基础等比数列） 数列： 3, 6, 12, 24, ( ) 解析： 这是一个典型的等比数列，后项除以前项的商均为2。 6 / 3 = 2 12 / 6 = 2 24 / 12 = 2 括号内的数字应为 24 × 2 = 48。

例题5（等比数列变式） 数列： 2, 3, 7, 16, 65, ( ) 解析：

1. 尝试作商：增长速度很快，考虑作商。 3 / 2 = 1.5 7 / 3 ≈ 2.33 16 / 7 ≈ 2.28 商没有规律,作商失败。
2. 尝试作差： 3 - 2 = 1 7 - 3 = 4 16 - 7 = 9 65 - 16 = 49
3. 观察新数列：得到的新数列是 1, 4, 9, 49，前三个数是平方数（1², 2², 3²），但第四个数7²=49,这个规律不统一。
4. 重新思考（混合规律）：观察数列 2, 3, 7, 16, 65，尝试寻找“乘加”规律。
   • 2 × 1 + 1 = 3
   • 3 × 2 + 1 = 7
   • 7 × 2 + 2 = 16 (这里规律开始变化)
   • 16 × 4 + 1 = 65 (规律不明显)
5. 再尝试另一种混合规律：观察 2, 3, 7, 16, 65。
   • 2² + 3 = 7
   • 3² + 7 = 16
   • 7² + 16 = 49 + 16 = 65 找到了！ 规律是：第三项 = 第一项² + 第二项。
6. 推导与求解：
   • 根据规律，下一项应为：16² + 65 = 256 + 65 = 321。
   • 所以括号内的数字是 321。

幂次数列

指数列的项与平方数、立方数等幂次相关,需要熟记常见的幂次。

例题6（平方数列） 数列： 1, 4, 9, 16, 25, ( ) 解析： 这是最基础的平方数列。 1 = 1² 4 = 2² 9 = 3² 16 = 4² 25 = 5² 括号内的数字应为 6² = 36。

例题7（立方数列变式） 数列： 0, 7, 26, 63, 124, ( ) 解析：

1. 观察数字：0, 7, 26, 63, 124，这些数字都接近某个整数的立方。
   • 0 = 1³ - 1
   • 7 = 2³ - 1
   • 26 = 3³ - 1
   • 63 = 4³ - 1
   • 124 = 5³ - 1
2. 总结规律：规律是 n³ - 1,其中n从1开始递增。
3. 求解：括号内是第6项，应为 6³ - 1 = 216 - 1 = 215。

递推数列

指后一项由前两项或前三项通过某种运算得到，最经典的是“斐波那契数列”及其变式。

例题8（和数列） 数列： 1, 2, 3, 5, 8, 13, ( ) 解析： 这是典型的和数列（斐波那契数列）。 从第三项开始，每一项都等于它前面两项之和。 3 = 1 + 2 5 = 2 + 3 8 = 3 + 5 13 = 5 + 8 括号内的数字应为 8 + 13 = 21。

例题9（差数列） 数列： 5, 3, 2, -1, -3, ( ) 解析：

1. 观察：数列单调递减，考虑作差。 5 - 3 = 2 3 - 2 = 1 2 - (-1) = 3 -1 - (-3) = 2 得到新数列 2, 1, 3, 2,无明显规律。
2. 尝试递推：观察 5, 3, 2, -1, -3。
   • 5 - 3 = 2 (第三项)
   • 3 - 2 = 1 (不是第四项-1)
   • 2 - (-1) = 3 (不是第五项-3) 规律不成立。
3. 重新思考（隔项递推）：
   • 第三项 = 第一项 - 第二项 = 5 - 3 = 2
   • 第四项 = 第二项 - 第三项 = 3 - 2 = 1 (但实际是-1,不符合)
4. 再思考（加减混合）：
   • 第三项 = 第一项 - 第二项 = 5 - 3 = 2
   • 第四项 = 第二项 - 第三项 = 3 - 2 = 1 (不符合)
   • 换一种方式：第三项 = 第二项 - 第一项 = 3 - 5 = -2 (不符合)
5. 最终发现（复杂递推）：
   • 第三项 = 第一项 - 第二项 = 5 - 3 = 2
   • 第四项 = 第二项 - 第三项 = 3 - 2 = 1 (不符合)
   • 等等，我们再看一次：5, 3, 2, -1, -3
   • 规律可能是：后一项 = 前一项 - 前前一项。
   • 2 = 3 - 1 (不对)
   • 让我们换一个思路：后一项 = 前前一项 - 前一项。
   • 2 = 5 - 3
   • -1 = 3 - 2 (符合)
   • -3 = 2 - (-1) = 3 (不符合) 这个规律也不完全对。
6. 正确解法（作差后分组）：
   • 对原数列作差：5, 3, 2, -1, -3
   • 一级差数列：3-5=-2, 2-3=-1, -1-2=-3, -3-(-1)=-2，得到 -2, -1, -3, -2。
   • 这个差数列依然不明显。
   • 回到原数列，重新观察：5, 3, 2, -1, -3，我们发现，从第三项开始,似乎每一项都是前两项的差。
   • 2 = 5 - 3
   • -1 = 3 - 2 (这里出现矛盾，应该是 -1 = 3 - 4？)
   • 看来这个数列规律性不强，可能是为了举例，我们换一个更经典的递推题。

经典递推题修正版： 数列： 3, 5, 8, 13, 21, ( ) 解析： 这是标准的和数列（斐波那契数列）。 从第三项开始，每一项等于前两项之和。 8 = 3 + 5 13 = 5 + 8 21 = 8 + 13 括号内的数字应为 13 + 21 = 34。

分数数列

分数数列的难点在于分子和分母各自有独立的规律,或者分子分母之间存在运算关系。

例题10（分子分母分别成规律） 数列： 1/2, 3/4, 5/8, 7/16, ( ) 解析： 将分子和分母分开来看。

• 分子数列：1, 3, 5, 7, ... 这是一个公差为2的等差数列，下一个分子是 7 + 2 = 9。
• 分母数列：2, 4, 8, 16, ... 这是一个公比为2的等比数列，下一个分母是 16 × 2 = 32。
• 组合：将分子和分母组合起来，括号内的数字是 9/32。

例题11（通分后找规律） 数列： 1/3, 1/2, 3/5, 2/3, 5/7, ( ) 解析：

1. 观察：分数形式不统一，尝试将所有分数化为分母相同的形式。
   • 1/3 = 10/30
   • 1/2 = 15/30
   • 3/5 = 18/30
   • 2/3 = 20/30
   • 5/7 ≈ 21.4/30 (分母不是30,此路不通)
2. 换一种思路（化小数）：
   • 1/3 ≈ 0.33
   • 1/2 = 0.5
   • 3/5 = 0.6
   • 2/3 ≈ 0.67
   • 5/7 ≈ 0.71 数列是 33, 0.5, 0.6, 0.67, 0.71，呈缓慢增长趋势,但增长幅度不固定。
3. 正确解法（分子分母分别找规律）：
   • 分子数列：1, 1, 3, 2, 5, ... 规律不明显。
   • 分母数列：3, 2, 5, 3, 7, ... 规律不明显。
   • 尝试交叉找规律：
     • 分子：1, 1, 3, 2, 5，可以看作 1, 1, 2+1, 2, 3+2,不明显。
     • 分母：3, 2, 5, 3, 7，可以看作 3, 2, 3+2, 3, 5+2,不明显。
4. 再次观察（分数性质）：
   • 1/3, 1/2, 3/5, 2/3, 5/7
   • 我们尝试将相邻两个分数进行某种运算，相加：
     • 1/3 + 1/2 = 5/6
     • 1/2 + 3/5 = 11/10
     • 3/5 + 2/3 = 19/15
     • 2/3 + 5/7 = 29/21 结果 5/6, 11/10, 19/15, 29/21 依然复杂。
5. 最终发现（分子分母的和是规律）：
   • 1/3: 1+3=4
   • 1/2: 1+2=3
   • 3/5: 3+5=8
   • 2/3: 2+3=5
   • 5/7: 5+7=12 得到新数列 4, 3, 8, 5, 12，这个数列的规律是：奇数位（第1,3,5项）是4, 8, 12（公差为4的等差数列）；偶数位（第2,4项）是3, 5（公差为2的等差数列）。
   • 下一项（第6项）是偶数位，应为 5 + 2 = 7。
   • 我们需要找一个分数，其分子分母之和为7，观察选项，如果选项中有 3/4 (3+4=7) 或 4/3 (4+3=7),则可能是答案。
   • 这个题目的规律非常隐蔽，在实际考试中，如果30秒内找不到，应果断放弃。

总结与备考建议

1. 基础为王：熟练掌握等差、等比、幂次、递推这四大基础数列及其变式，80%的题目都源于此。
2. 思维要活：不要局限于一种方法，作差作商是首选，但不行就要立刻想到分组、拆分、递推等其他思路。
3. 敏感度培养：对数字要敏感，看到 1, 4, 9, 16 要立刻想到平方；看到 2, 6, 18, 54 要立刻想到等比；看到 1, 1, 2, 3, 5 要立刻想到和数列。
4. 大量练习：这是提高速度和准确率唯一的方法，通过做题，你才能在看到数列的瞬间,条件反射般地想到最可能的规律。
5. 学会放弃：国考行测时间非常紧张，如果一个数列题思考超过1分钟还没有头绪，果断标记并跳过,把时间留给更有把握的题目。

希望这份详细的解析对你有帮助！祝你备考顺利,金榜题名！