下面我将从模块概述、核心考点、解题策略、备考建议四个方面为你进行详细拆解。
模块概述
-
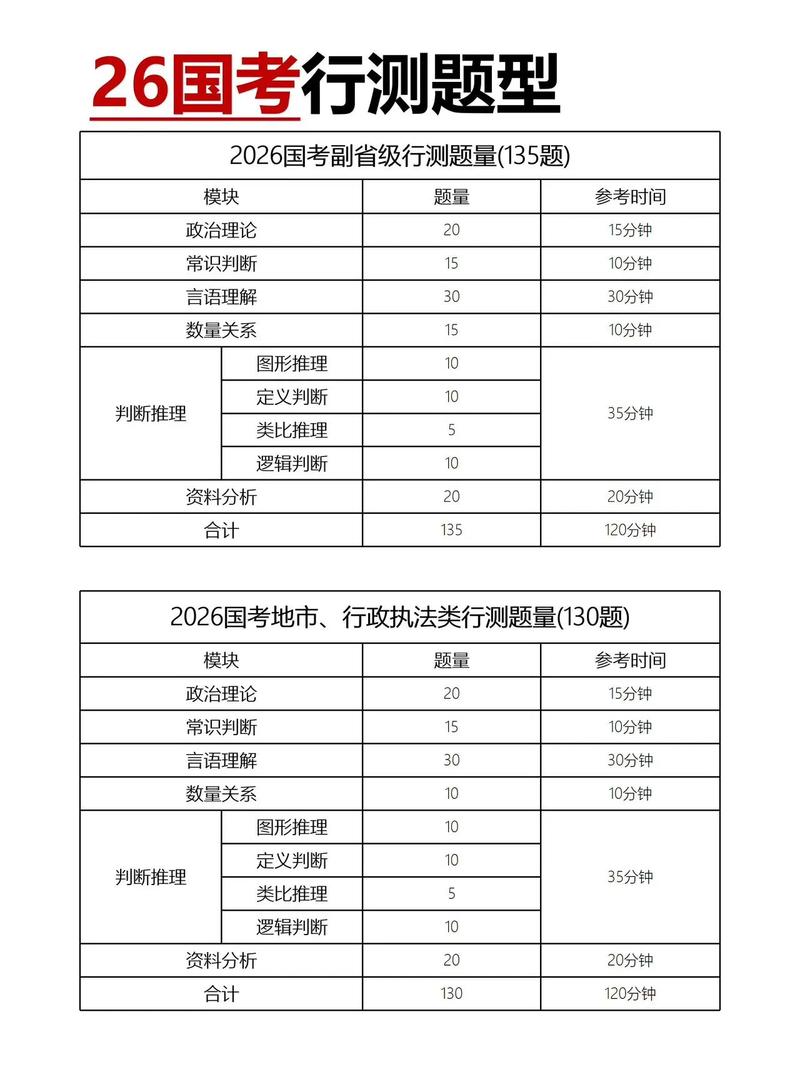
题量与分值:
 (图片来源网络,侵删)
(图片来源网络,侵删)- 国考副省级和地市级试卷的题量略有不同。
- 副省级:通常为 15道 题目。
- 地市级:通常为 10道 题目。
- 分值每道题约在0.6-0.8分之间,总分值占比不低,是拉开差距的关键。
-
考试形式:
- 全部为单项选择题。
- 题目以文字应用题为主,辅以少量纯数字推理(近两年国考已基本不考数字推理,以应用题为主)。
-
核心特点:
- 时间紧:平均每道题的解题时间需要控制在1分钟以内,部分难题可能需要更长时间,因此简单题必须快速解决。
- 难度适中:题目难度介于小学奥数和初中数学竞赛之间,但考察的是在高压环境下快速理解和解决问题的能力。
- 重思维,轻计算:考察的是逻辑分析、数学建模和巧算能力,而非复杂的数值计算,一道题如果用笨方法算,可能5分钟也算不完,但用巧方法可能30秒就出答案。
核心考点与题型
数量关系考点非常集中,掌握以下几大核心题型,就能覆盖绝大部分题目。
第一梯队:高频必考(约占总题量的70%)
-
工程问题
 (图片来源网络,侵删)
(图片来源网络,侵删)- 核心公式:工作总量 = 工作效率 × 工作时间。
- 解题关键:
- 赋值法:当题目中没有给出具体总量时,通常将总量赋值为一个方便计算的值(如效率的最小公倍数、1、100等)。
- 比例关系:在总量一定的情况下,效率和时间成反比。
- 常见题型:多人合作、轮流工作、效率变化等。
-
行程问题
- 核心公式:路程 = 速度 × 时间。
- 关键考点:
- 基本公式:追及问题(路程差=速度差×时间)、相遇问题(路程和=速度和×时间)。
- 比例关系:在时间一定时,路程和速度成正比;在路程一定时,速度和时间成反比。
- 平均速度:平均速度 = 总路程 / 总时间,不等于 速度的算术平均值。
- 流水行船:顺水速度 = 船速 + 水速,逆水速度 = 船速 - 水速。
- 常见题型:多次相遇、环形路线、火车过桥等。
-
利润问题
- 核心公式:
- 利润 = 售价 - 成本
- 利润率 = 利润 / 成本 (注意是相对于成本而言)
- 售价 = 成本 × (1 + 利润率)
- 打折:折扣后的售价 = 原价 × 折扣率(如8折就是0.8)
- 解题关键:找准“单位1”(即成本),分清利润和利润率,注意“打折”和“利润率”的区别。
- 核心公式:
-
排列组合与概率问题
- 排列组合:
- 核心概念:分类(用加法)、分步(用乘法)。
- 常用公式:
- 排列(与顺序有关):A(n, m) = n! / (n-m)!
- 组合(与顺序无关):C(n, m) = n! / [m! * (n-m)!]
- 解题技巧:特殊元素优先法、捆绑法、插空法、隔板法(针对分配问题)。
- 概率问题:
- 核心公式:概率 = 满足条件的情况数 / 所有可能的情况数。
- 解题关键:分清事件是独立事件还是互斥事件,利用对立面(反面)简化计算。
- 排列组合:
第二梯队:中频常考(约占总题量的20%)
-
容斥原理
 (图片来源网络,侵删)
(图片来源网络,侵删)- 核心思想:用集合的并集来计算重叠部分。
- 解题技巧:画文氏图(Venn Diagram)是解题最直观的方法。
- 常用公式:
- |A ∪ B| = |A| + |B| - |A ∩ B|
- |A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|
-
几何问题
- 核心考点:
- 平面几何:三角形、四边形、圆形的周长、面积公式。
- 立体几何:正方体、长方体、圆柱体、球体的表面积、体积公式。
- 几何特性:相似三角形的性质、勾股定理、等量代换(如“将军饮马”模型)。
- 解题技巧:割补法、等面积转换、特殊值法。
- 核心考点:
-
浓度问题
- 核心公式:浓度 = 溶质质量 / 溶液质量。
- 解题关键:抓住“溶质”不变这个核心,通过方程或十字交叉法解决,多次稀释问题,可以记住结论:设原有溶液为1,每次加水a,稀释n次后,浓度为原浓度的 (1/(1+a))^n。
第三梯队:低频或偶考
-
不定方程
- 特点:未知数个数多于方程个数,有无数解,但在公务员考试中,要求解的是正整数解。
- 解题技巧:奇偶性、整除性、尾数特性、代入排除法。
-
年龄问题
- 核心特点:年龄差值不变。
- 解题关键:抓住“年龄差”这个不变量,通过差倍关系或设未知数列方程来解决。
-
牛吃草问题
- 核心模型:原有草量 = (牛吃草速度 - 草生长速度) × 吃光时间。
- 解题技巧:公式法或赋值法,将草的生长速度和牛的吃草速度进行对比。
解题策略与技巧
-
代入排除法:
- 第一优先级,当选项信息明确(尤其是数字选项)或正面计算复杂时,直接将选项代入题干验证,能极大节省时间,尤其适用于多位数问题、年龄问题、不定方程等。
-
赋值法:
- 第二优先级,当题目中缺少某个具体量(如总量、效率、速度、具体人数)时,可以给这个量赋一个方便计算的值(如1、10、100),从而简化计算,常用于工程问题、行程问题、利润问题。
-
方程法:
- 万能但非最优,对于关系复杂、难以用算术方法解决的问题,设未知数列方程是稳妥的选择,但要注意设未知数的技巧(设“单位1”或设中间量为未知数),并尽量使用一元一次方程。
-
整除特性法:
- 快速判断选项,根据题干中的关键信息(如“平均分配”、“每份”、“倍数”等),判断结果应该具备的整除特性(如能被3、5、9整除等),从而排除错误选项。
-
特值/极端情况法:
用于解决一些抽象或复杂的比较问题,通过设定一个满足条件的特殊数值(如让某个量为0或1),来快速验证选项。
-
十字交叉法:
- 速算神器,主要用于解决混合平均问题,如溶液混合、平均数、利润率混合等,能快速求出混合前两部分的比例关系。
备考建议
-
打牢基础(1-2周):
- 系统学习所有核心考点的公式、概念和解题模型。
- 做好笔记,整理每个题型的特征和解题“套路”。
-
专项突破(2-3周):
- 按题型进行大量刷题,特别是第一梯队的四大题型。
- 做题后一定要复盘:这道题用了什么方法?有没有更快的解法?为什么我当时没想到?把错题和好题整理到错题本中。
-
套题演练(持续进行):
- 严格按照考试时间(建议20-25分钟内完成)做完整的套题。
- 目的是训练时间分配能力和考场心态,学会在压力下做出取舍。
-
总结归纳(贯穿始终):
- 定期回顾错题本,总结自己的薄弱环节。
- 归纳同类型题目的共性,形成自己的解题体系。
最后心态调整: 数量关系是“性价比”和“投入产出比”很高的模块,对于大部分考生,目标是做对60%-70%的题目即可,不必强攻所有难题,学会取舍,如果一道题1分钟内没有思路,果断标记并跳过,把时间留给更有把握的题目。
祝你备考顺利,成功上岸!











